Estructuras de datos para la representación de grafos
Existen 2 estructuras de datos muy conocidas para la representación de grafos. Estas son:
Lista de vértice – Matriz de adyacencia y Lista vértices – Lista de adyacencia
1- Lista de vértice – Matriz de adyacencia
1.1- Grafo no dirigido y no ponderado.
La forma más sencilla de representar un grafo es usando una lista de vértices que almacena los vértices y una matriz que almacena las aristas.
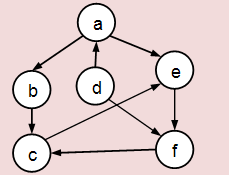
Fig. 1 Grafo no dirigido no ponderado
Para mostrar de una forma sencilla como es la representación hagámoslo con el grafo de la figura 1.
La lista de vértices del grafo es L = {a,b,c,d,e,f}
La matriz de adyacencia estaría compuesta por una tabla de 6x6, la dimensión de la matriz es el número de vértices del grafo. Gráficamente se vería como muestra en la figura 2.

Fig.2 Matriz de adyacencia
Esta matriz contiene las aristas del grafo, el ejemplo de la figura 1 es de tipo No ponderado, No dirigido. Los ceros indican que no existen aristas entre las componentes Fila – Columna, por ejemplo en la intersección del vértice a – c hay un cero pues no hay arista entre a y c ; pero también hay un cero en la intercepción c - a . Recordemos que cuando el grafo no es dirigido no hay diferencia entre un arco de la forma <a,b> y <b,a>
Cuando existe un arco entre 2 vértices entonces se coloca el valor 1. Ejemplo <a,b> y <b,a>
1.2- Grafo no dirigido, ponderado

Fig. 3 Grafo no dirigido ponderado
En el caso de un grafo ponderado lo único que cambia es que en vez de colocar un 1 en las intercepciones de aristas, se coloca el peso que posee dicha arista.
La lista de vértices de este grafo L = {a,b,c,d,e,f}
La matriz de adyacencia se vería como muestra en la figura 4.

Fig.4 Matriz de adyacencia para grafo ponderado
1.3- Grafo dirigido, no ponderado.

Fig.5 Grafo dirigido no ponderado
En un Grafo dirigido hay que tener en cuenta el orden de las aristas, para este grafo de la figura 5 , existe la arista formada por el par <a,b>; pero no existe <b,a> . Por lo tanto en la matriz se debe colocar un 1 solo en el par <a,b> y un cero en el par <b,a>. Ver en la figura 6 que existe el valor uno (1) en la intercepción fila (a) y columna (b); sin embargo en la intercepción fila (b) y columna (a) hay un cero (0)
La lista de vértices de este grafo L = {a,b,c,d,e,f}
La matriz de adyacencia se vería como muestra en la figura 6.

Fig.6 Grafo dirigido no ponderado
1.4- Grafo dirigido, ponderado.
Ya debes imaginar cómo representar un Grafo dirigido y ponderado. Simplemente igual al Grafo dirigido y no ponderado, solo cambia el uno (1) por el peso de las aristas en los valores de la matriz. Ver el ejemplo de la figura 7 representado en tabla

Fig.7 Grafo dirigido ponderado
La lista de vértices de este grafo L = {a,b,c,d,e,f}
La matriz de adyacencia se vería como muestra en la figura 8.

Fig.8 Matriz de adyacencia en el grafo dirigido ponderado
2- Lista de vértice – Lista de adyacencia
Otra estructura de datos que se utiliza para los grafos es la Lista de vértice – Lista de adyacencia. En esta se estructura se utiliza una lista de vértices al igual que en Lista de vértice – Matriz de adyacencia; pero no se utiliza una matriz sino una lista de listas de vértices en la que se almacenan las relaciones entre vértices que como ya sabemos son los arcos o aristas.
En esta representación con Lista de adyacencia solo veremos los ejemplos de grafos no dirigidos, no ponderado y no dirigido ponderado ya que las otras 2 combinaciones son en esencia iguales. Lo diferencia solo la da si el grafo es ponderado o no pues esta condición como se verá adelante cambia la estructura de dato, no siendo así con si es dirigido o no dirigido.
2.1- Grafo no dirigido y no ponderado.

Fig. 9 Grafo no dirigido no ponderado
Veamos como resultaría la estructura para el grafo de figura 9.
En la figura 10 de abajo, vemos la representación grafica de la lista de vértices, pero hemos en este caso representado también las posiciones de cada vértice en la lista, pues esta posición tendrá mucha importancia en la lista de adyacencia. Las posiciones comienzan en 0 ya que por lo general todas las listas que se usan en cualquier lenguaje de programación comienzan en posición 0, aunque en teóricamente en muchos libros la primera posición es 1. Por consenso siempre asumo que las listas comienzan en 0 para no chocar en la práctica con otra realidad. Esto ha sido causa de muchas discusiones entre mis colegas; pero yo soy más práctico que teórico.

Fig.10 Lista de vértices y sus posiciones
En la figura 11 vemos la representación de la lista de adyacencia, la explico en detalles a continuación:
Una lista de adyacencia es una lista de lista, es decir una lista donde cada elemento posee otro listado con los vértices adyacentes.
Como ya vimos en la figura 10 cada vértice tiene asociado una posición en la lista de vértices, por lo tanto el vértice (a) tiene posición cero (0) , el (b)=> (1) y así sucesivamente.
Ahora sigue con la vista la figura 11, lo que ves es una lista de listas , la primera fila o la lista que está en posición (0) contiene los vértices que poseen arista con el vértice (a) recordemos que el vértice (a) en la Lista de vértices tiene posición (0) , veremos que en esa lista aparecen los siguientes números: (1),(3),(4) ; estos son las posiciones correspondientes a los vértices adyacentes (que tiene aristas) con el vértice (a) que son : (b) , (d) y (e).
Entonces de seguro ya te das cuenta cómo funciona esta estructura, la segunda lista contiene las posiciones los vértices adyacentes a al vértice (b) y así sucesivamente hasta el último vértice en la lista que el (f).

Fig.11 Lista de adyacencia
2.2- Grafo no dirigido y ponderado.
La representación del grafo ponderado en Lista de vértice – Lista de adyacencia, tiene una diferencia en cuanto a lo que almacenamos en la lista de lista o lista de adyacencia; la razón es muy simple y es que necesitamos almacenar también el peso de las aristas por lo que necesitaremos construir una estructura que sea capaz de hacer esto

Fig. 12 Grafo no dirigido ponderado
Pues la explicación en las misma que con el grafo anterior pero en vez de almacenar las posición de los vértices adyacente en la lista de lista, debemos crear un estructura que contenga la posición y el peso. Por ejemplo ahora los adyacentes al vértice (a) que es la posición (0) siguen siendo (1),(3),(4) es decir los vértices (b) ,(d), (e). Pero el peso con el vértice (1) es 2 por eso en la representación grafica de la figura 13, dividimos las celdas de la lista en dos partes la primera es la posición del vértice y la segunda en negro el peso.

Fig.13 Lista de adyacencia
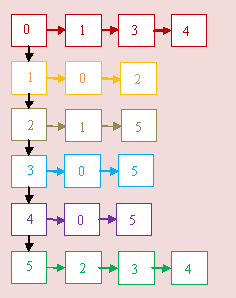
Fig.14 Lista de vértices
Lista de vértice – Matriz de adyacencia y Lista vértices – Lista de adyacencia
1- Lista de vértice – Matriz de adyacencia
1.1- Grafo no dirigido y no ponderado.
La forma más sencilla de representar un grafo es usando una lista de vértices que almacena los vértices y una matriz que almacena las aristas.

Fig. 1 Grafo no dirigido no ponderado
Para mostrar de una forma sencilla como es la representación hagámoslo con el grafo de la figura 1.
La lista de vértices del grafo es L = {a,b,c,d,e,f}
La matriz de adyacencia estaría compuesta por una tabla de 6x6, la dimensión de la matriz es el número de vértices del grafo. Gráficamente se vería como muestra en la figura 2.

Fig.2 Matriz de adyacencia
Esta matriz contiene las aristas del grafo, el ejemplo de la figura 1 es de tipo No ponderado, No dirigido. Los ceros indican que no existen aristas entre las componentes Fila – Columna, por ejemplo en la intersección del vértice a – c hay un cero pues no hay arista entre a y c ; pero también hay un cero en la intercepción c - a . Recordemos que cuando el grafo no es dirigido no hay diferencia entre un arco de la forma <a,b> y <b,a>
Cuando existe un arco entre 2 vértices entonces se coloca el valor 1. Ejemplo <a,b> y <b,a>
1.2- Grafo no dirigido, ponderado

Fig. 3 Grafo no dirigido ponderado
En el caso de un grafo ponderado lo único que cambia es que en vez de colocar un 1 en las intercepciones de aristas, se coloca el peso que posee dicha arista.
La lista de vértices de este grafo L = {a,b,c,d,e,f}
La matriz de adyacencia se vería como muestra en la figura 4.

Fig.4 Matriz de adyacencia para grafo ponderado
1.3- Grafo dirigido, no ponderado.

Fig.5 Grafo dirigido no ponderado
En un Grafo dirigido hay que tener en cuenta el orden de las aristas, para este grafo de la figura 5 , existe la arista formada por el par <a,b>; pero no existe <b,a> . Por lo tanto en la matriz se debe colocar un 1 solo en el par <a,b> y un cero en el par <b,a>. Ver en la figura 6 que existe el valor uno (1) en la intercepción fila (a) y columna (b); sin embargo en la intercepción fila (b) y columna (a) hay un cero (0)
La lista de vértices de este grafo L = {a,b,c,d,e,f}
La matriz de adyacencia se vería como muestra en la figura 6.

Fig.6 Grafo dirigido no ponderado
1.4- Grafo dirigido, ponderado.
Ya debes imaginar cómo representar un Grafo dirigido y ponderado. Simplemente igual al Grafo dirigido y no ponderado, solo cambia el uno (1) por el peso de las aristas en los valores de la matriz. Ver el ejemplo de la figura 7 representado en tabla

Fig.7 Grafo dirigido ponderado
La lista de vértices de este grafo L = {a,b,c,d,e,f}
La matriz de adyacencia se vería como muestra en la figura 8.

Fig.8 Matriz de adyacencia en el grafo dirigido ponderado
2- Lista de vértice – Lista de adyacencia
Otra estructura de datos que se utiliza para los grafos es la Lista de vértice – Lista de adyacencia. En esta se estructura se utiliza una lista de vértices al igual que en Lista de vértice – Matriz de adyacencia; pero no se utiliza una matriz sino una lista de listas de vértices en la que se almacenan las relaciones entre vértices que como ya sabemos son los arcos o aristas.
En esta representación con Lista de adyacencia solo veremos los ejemplos de grafos no dirigidos, no ponderado y no dirigido ponderado ya que las otras 2 combinaciones son en esencia iguales. Lo diferencia solo la da si el grafo es ponderado o no pues esta condición como se verá adelante cambia la estructura de dato, no siendo así con si es dirigido o no dirigido.
2.1- Grafo no dirigido y no ponderado.

Fig. 9 Grafo no dirigido no ponderado
Veamos como resultaría la estructura para el grafo de figura 9.
En la figura 10 de abajo, vemos la representación grafica de la lista de vértices, pero hemos en este caso representado también las posiciones de cada vértice en la lista, pues esta posición tendrá mucha importancia en la lista de adyacencia. Las posiciones comienzan en 0 ya que por lo general todas las listas que se usan en cualquier lenguaje de programación comienzan en posición 0, aunque en teóricamente en muchos libros la primera posición es 1. Por consenso siempre asumo que las listas comienzan en 0 para no chocar en la práctica con otra realidad. Esto ha sido causa de muchas discusiones entre mis colegas; pero yo soy más práctico que teórico.

Fig.10 Lista de vértices y sus posiciones
En la figura 11 vemos la representación de la lista de adyacencia, la explico en detalles a continuación:
Una lista de adyacencia es una lista de lista, es decir una lista donde cada elemento posee otro listado con los vértices adyacentes.
Como ya vimos en la figura 10 cada vértice tiene asociado una posición en la lista de vértices, por lo tanto el vértice (a) tiene posición cero (0) , el (b)=> (1) y así sucesivamente.
Ahora sigue con la vista la figura 11, lo que ves es una lista de listas , la primera fila o la lista que está en posición (0) contiene los vértices que poseen arista con el vértice (a) recordemos que el vértice (a) en la Lista de vértices tiene posición (0) , veremos que en esa lista aparecen los siguientes números: (1),(3),(4) ; estos son las posiciones correspondientes a los vértices adyacentes (que tiene aristas) con el vértice (a) que son : (b) , (d) y (e).
Entonces de seguro ya te das cuenta cómo funciona esta estructura, la segunda lista contiene las posiciones los vértices adyacentes a al vértice (b) y así sucesivamente hasta el último vértice en la lista que el (f).

Fig.11 Lista de adyacencia
2.2- Grafo no dirigido y ponderado.
La representación del grafo ponderado en Lista de vértice – Lista de adyacencia, tiene una diferencia en cuanto a lo que almacenamos en la lista de lista o lista de adyacencia; la razón es muy simple y es que necesitamos almacenar también el peso de las aristas por lo que necesitaremos construir una estructura que sea capaz de hacer esto

Fig. 12 Grafo no dirigido ponderado
Pues la explicación en las misma que con el grafo anterior pero en vez de almacenar las posición de los vértices adyacente en la lista de lista, debemos crear un estructura que contenga la posición y el peso. Por ejemplo ahora los adyacentes al vértice (a) que es la posición (0) siguen siendo (1),(3),(4) es decir los vértices (b) ,(d), (e). Pero el peso con el vértice (1) es 2 por eso en la representación grafica de la figura 13, dividimos las celdas de la lista en dos partes la primera es la posición del vértice y la segunda en negro el peso.

Fig.13 Lista de adyacencia

Fig.14 Lista de vértices

Comentarios
Publicar un comentario