Recorridos en grafos
Estos recorridos pueden ser usados en distintos algoritmos para la solución de problemas particulares.
Recorrido en profundidad
Definición del método:RecorrerEnProfundidad (RP)
Para cada v que pertenece a la lista de vértices; marcar v como no visitado
Para cada v que pertenece a la lista de vértices hacer:
Si v no está visitado
Entonces BPP(v)
Luego el método BPP realiza las siguientes acciones:
Adicionar al recorrido
Marcar v como visitado
Para cada vértice w adyacente a v hacer:
Si w no está visitado entonces BPP(w) // esta es al recursividad
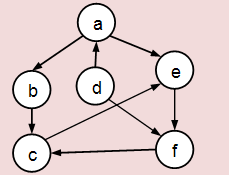
A continuación un ejemplo de este recorrido sobre el grafo de la figura 1.
Fig. 1 Grafo ejemplo
Árbol de las llamadas recursivas al método Búsqueda en Profundidad del Primero BPP(v).
Fig. 2 Gráfico del recorrido en profundidad del grafo de la figura 1
En la siguiente tabla se muestran las llamadas recursivas del ejercicio, en la primera columna las llamadas recursivas del método BPP, en la segunda columna los vértices adyacentes del vértice que llamamos en el método BPP y noten que se pintan en rojo los que ya están marcado, es decir lo que ya están en el recorrido que se muestra en la tercera columna:
Tabla de que representan las llamadas recursivas.
De las llamadas recursivas se forman y o varios árboles en dependencia del grafo donde el nodo padre es el vértice que estamos llamando en el método BPP y los subArboles o hijos son los vértices adyacentes al padre y que no están marcados aun , es decir no están aun en el recorrido . Y curiosamente la unión de los recorridos en preOrden, forman el recorrido en profundidad del grafo:
Fig. 2 Árboles de llamadas BPP
Recorridos PreOrden de los arboles:
a) a, b, c, f
b) e
Y al unir los recorridos comenzando por el primero nos queda: a, b, c, f, d, e. El recorrido en profundidad del grafo.
Recorrido a lo ancho
Definición del método: RecorrerAncho (RP)
Paso 1 (Inicialización):
Para cada vértice (v) que pertenece a la lista de vértices (V)
Marcar a v como no visitado.
Paso 2 (Recorrido):
Para cada v pertenece a V,
Si v no está visitado entonces
Hacer la Búsqueda del Primero a lo Ancho (BPA) partiendo por v.
El algoritmo de la BPA es un algoritmo que recibe como parámetro un vértice v del grafo. No es recursivo, y para su ejecución se auxilia de una instancia del TDA Cola, que sería una cola de vértices. El algoritmo BPA(v) presenta los siguientes pasos:
Paso 1: Inicializar Cola vacía
Paso 2: Marcar v como visitado.
Paso 3: Adicionar v a Cola.
Paso 4: Mientras Cola no es vacía hacer
4.1) Extraer un vértice de Cola. Sea u el vértice extraído.
4.2) Para cada w adyacente a u hacer
4.2.1) Si w no está visitado entonces
4.2.1.1) Marcar w como visitado
4.2.1.2) Adicionar w a Cola.
En la figura 3 se muestra la representación de un recorrido a la ancho de un grafo mostrando paso por paso el estado de la cola en las llamadas al método BPA. 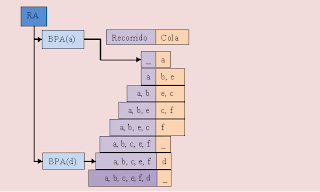
Fig. 3 Recorrido a lo ancho
Comentarios
Publicar un comentario