Programación de estructuras de datos

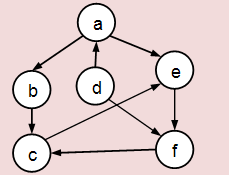
Existen 2 estructuras de datos muy conocidas para la representación de grafos. Estas son: Lista de vértice – Matriz de adyacencia y Lista vértices – Lista de adyacencia 1- Lista de vértice – Matriz de adyacencia 1.1- Grafo  no dirigido y no ponderado. La forma más sencilla de representar un grafo es usando una lista de vértices que almacena los vértices y una matriz que almacena las aristas. Fig. 1 Grafo no dirigido no ponderado Para mostrar de una forma sencilla como es la representación hagámoslo con  el grafo de la figura 1. La lista de vértices del grafo es L = {a,b,c,d,e,f} La matriz de adyacencia   estaría compuesta por una tabla de 6x6, la dimensión de la matriz es el número de  vértices del grafo. Gráficamente se vería como muestra  en la figura 2.  Fig.2 Matriz de adyacencia Esta matriz contiene las aristas del grafo, el ejemplo de la figura 1 es de tipo No ponderado, No dirigido.   Los ceros indican que no existen aristas entre las componentes Fila – C...

En este artículo  vernos 2 recorridos distintos que se pueden realizar sobre los grafos. Los recorridos son algoritmos que se llevan a cabo sobre el grafo y que devuelven una lista de vértices con todos los vértices del grafo. Estos recorridos pueden ser usados en distintos algoritmos para la solución de problemas particulares.   Recorrido en profundidad Definición del método: RecorrerEnProfundidad (RP) Para cada v que pertenece a la lista de  vértices;  marcar v como no visitado Para cada v que pertenece a la lista de  vértices hacer: Si v no está visitado                Entonces BPP(v) Luego el método BPP realiza las siguientes acciones: Adicionar al recorrido Marcar v como visitado Para cada vértice w adyacente a v hacer: Si w no está visitado entonces BPP(w)  // esta es al recursividad A continuación un ejemplo de este recorrido sobre el grafo de la figura 1. Fig. 1 Grafo ejemplo Árbol de las llamadas recursivas al método Búsqueda en Profundidad del Primero BPP(v...

En múltiples problemas computacionales y de la vida práctica también se necesitaran establecer relaciones que sean simétricas y que provoquen ciclos en la estructura. Por ejemplo "X es amigo de Y". Ver fig. 1 Fig.1 Relación de amistad Primer Registro Histórico de del origen de los grafos Se dice que el primero en trabajar con de grafos fue el famoso matemático Leonhard Euler en 1736. En la ciudad de Kaliningrado (antigua Königsberg) había siete puentes sobre el río Pregel. Estos se conectaban como se muestra en la figura 2. Euler se preguntó si sería posible comenzar un paseo desde cualquier punto y atravesar cada puente una y sólo una vez, regresando al punto departida. Al final de este artículo vernos la solución de que Euler encontró a este problema, por medio de un grafo. Fig.2 Los puentes de Königsberg Definición de grafo Un grafo G es un par G = (V, A) donde V es un conjunto finito de elementos que se denominan Vértices y A es un conjunto de pares no ordenados ...