Definición y orígenes de los grafos
En múltiples problemas computacionales y de la vida práctica también se necesitaran establecer relaciones que sean simétricas y que provoquen ciclos en la estructura. Por ejemplo "X es amigo de Y". Ver fig. 1

Fig.1 Relación de amistad
Primer Registro Histórico de del origen de los grafos
Se dice que el primero en trabajar con de grafos fue el famoso matemático Leonhard Euler en 1736.
En la ciudad de Kaliningrado (antigua Königsberg) había siete puentes sobre el río Pregel. Estos se conectaban como se muestra en la figura 2.
Euler se preguntó si sería posible comenzar un paseo desde cualquier punto y atravesar cada puente una y sólo una vez, regresando al punto departida.
Al final de este artículo vernos la solución de que Euler encontró a este problema, por medio de un grafo.
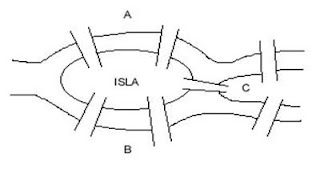
Fig.2 Los puentes de Königsberg
Definición de grafo
Un grafo G es un par G = (V, A) donde V es un conjunto finito de elementos que se denominan Vértices y A es un conjunto de pares no ordenados <x,y>, donde x pertenece a V y y pertenece a V, denominados Aristas o Arcos.

Fig.3 Ejemplo de grafo
Definición de Grafo Dirigido
Un grafo dirigido G es un par G = (V, A) donde V es un conjunto finito de elementos que se denominan Vértices y A es un conjunto de pares ordenados <x,y>, donde x pertenece a V y y pertenece a V, denominados Aristas o Arcos dirigidos.
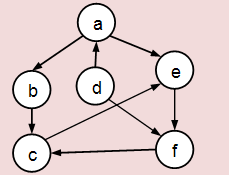
Para los grafos dirigidos tiene relevancia el orden en que se enuncian los vértices para describir una arista. Es decir, los pares <x,y> y <y,x> se refieren a aristas distintas. En la figura 4 se muestra un grafo dirigido.

Fig.4 Ejemplo de grafo dirigido
¿Qué es un Grafo Ponderado?
Un grafo ponderado G es un par G = (V, A) donde V es un conjunto finito de elementos que se denominan Vértices, A es un conjunto de pares no ordenados <x,y>, donde x pertenece a V , y pertenece a V, denominados Aristas o Arcos, donde a cada elemento de A (a cada arista) se le asocia un valor real positivo. En la figura 5 se muestra un grafo ponderado.

Fig.5 Ejemplo de grafo ponderado
El peso asociado a cada arista puede interpretarse como el costo de trasladarse de un vértice a otro. Dicho costo puede ser costo en tiempo, distancia, costo en algún determinado recurso, etc.
Terminologías utilizadas en los grafos
Vértices Adyacentes:
En un grafo G = (V, A), un vértice y es adyacente a otro vértice x si el par <x,y> es una arista del grafo G.

Fig.6 Ejemplo vértices adyacentes y no adyacentes
Camino:
En un grafo G = (V, A) un camino de longitud N (N >= 0) es una sucesión de vértices V0, V1, …, Vn donde cada vértice Vk es adyacente Vk-1 para 1 <= k <= N. En este caso se dice que el camino va de V0 a Vn.

Fig.7 Ejemplo de camino
Camino simple:
Un camino es simple si los vértices que lo componen son distintos excepto posiblemente el primero y el último.

Fig.8 Ejemplo de camino simple
Longitud de un camino:
La longitud de un camino es el número de arcos que lo componen. El camino en amarillo de la figura 8 tiene longitud 5.
Ciclo (o circuito):
Es un camino que empieza y acaba en el mismo vértice. Los ciclos de longitud 1 se denominan bucles.

Fig.9 Ejemplo de ciclos
Grafo conexo (conectado):
Un grafo es conexo si existe al menos un camino de cualquier vértice a cualquier otro.

Fig.10 Grafo conexo.
Solución de Euler a los puentes de Königsberg
Al convertir los puentes de Königsberg en un grafo queda como se muestra en la figura 11. Los puentes son las aristas y los vértices son las zonas de tierra.
Euler inteligentemente se percató de que el camino sin pasar 2 veces por una misma arista en un grafo (camino Euleriano) solo es posible cuando los vértices del grafo, salvo a lo más en dos, converjan un números pares de aristas. La razón es muy simple: al llegar a un vértice se necesita poder salir por una arista distinta a la que se llega, por lo tanto el número de aristas que convergen en un vértice debe ser par; pero esto no es necesario en el vértice inicial y el vértice final.
En el grafo formado por los puentes de Königsberg , a cada uno de los nodos concurre un número impar de aristas (3, 5, 3, 3). Por lo tanto es imposible realizar el paseo que Euler deseaba hacer en dichos puentes.

Fig. 11 Grafo que representa los puentes de Königsberg

Fig.1 Relación de amistad
Primer Registro Histórico de del origen de los grafos
Se dice que el primero en trabajar con de grafos fue el famoso matemático Leonhard Euler en 1736.
En la ciudad de Kaliningrado (antigua Königsberg) había siete puentes sobre el río Pregel. Estos se conectaban como se muestra en la figura 2.
Euler se preguntó si sería posible comenzar un paseo desde cualquier punto y atravesar cada puente una y sólo una vez, regresando al punto departida.
Al final de este artículo vernos la solución de que Euler encontró a este problema, por medio de un grafo.

Fig.2 Los puentes de Königsberg
Definición de grafo
Un grafo G es un par G = (V, A) donde V es un conjunto finito de elementos que se denominan Vértices y A es un conjunto de pares no ordenados <x,y>, donde x pertenece a V y y pertenece a V, denominados Aristas o Arcos.

Fig.3 Ejemplo de grafo
Definición de Grafo Dirigido
Un grafo dirigido G es un par G = (V, A) donde V es un conjunto finito de elementos que se denominan Vértices y A es un conjunto de pares ordenados <x,y>, donde x pertenece a V y y pertenece a V, denominados Aristas o Arcos dirigidos.
Para los grafos dirigidos tiene relevancia el orden en que se enuncian los vértices para describir una arista. Es decir, los pares <x,y> y <y,x> se refieren a aristas distintas. En la figura 4 se muestra un grafo dirigido.

Fig.4 Ejemplo de grafo dirigido
¿Qué es un Grafo Ponderado?
Un grafo ponderado G es un par G = (V, A) donde V es un conjunto finito de elementos que se denominan Vértices, A es un conjunto de pares no ordenados <x,y>, donde x pertenece a V , y pertenece a V, denominados Aristas o Arcos, donde a cada elemento de A (a cada arista) se le asocia un valor real positivo. En la figura 5 se muestra un grafo ponderado.

Fig.5 Ejemplo de grafo ponderado
El peso asociado a cada arista puede interpretarse como el costo de trasladarse de un vértice a otro. Dicho costo puede ser costo en tiempo, distancia, costo en algún determinado recurso, etc.
Terminologías utilizadas en los grafos
Vértices Adyacentes:
En un grafo G = (V, A), un vértice y es adyacente a otro vértice x si el par <x,y> es una arista del grafo G.

Fig.6 Ejemplo vértices adyacentes y no adyacentes
Camino:
En un grafo G = (V, A) un camino de longitud N (N >= 0) es una sucesión de vértices V0, V1, …, Vn donde cada vértice Vk es adyacente Vk-1 para 1 <= k <= N. En este caso se dice que el camino va de V0 a Vn.

Fig.7 Ejemplo de camino
Camino simple:
Un camino es simple si los vértices que lo componen son distintos excepto posiblemente el primero y el último.

Fig.8 Ejemplo de camino simple
Longitud de un camino:
La longitud de un camino es el número de arcos que lo componen. El camino en amarillo de la figura 8 tiene longitud 5.
Ciclo (o circuito):
Es un camino que empieza y acaba en el mismo vértice. Los ciclos de longitud 1 se denominan bucles.

Fig.9 Ejemplo de ciclos
Grafo conexo (conectado):
Un grafo es conexo si existe al menos un camino de cualquier vértice a cualquier otro.

Fig.10 Grafo conexo.
Solución de Euler a los puentes de Königsberg
Al convertir los puentes de Königsberg en un grafo queda como se muestra en la figura 11. Los puentes son las aristas y los vértices son las zonas de tierra.
Euler inteligentemente se percató de que el camino sin pasar 2 veces por una misma arista en un grafo (camino Euleriano) solo es posible cuando los vértices del grafo, salvo a lo más en dos, converjan un números pares de aristas. La razón es muy simple: al llegar a un vértice se necesita poder salir por una arista distinta a la que se llega, por lo tanto el número de aristas que convergen en un vértice debe ser par; pero esto no es necesario en el vértice inicial y el vértice final.
En el grafo formado por los puentes de Königsberg , a cada uno de los nodos concurre un número impar de aristas (3, 5, 3, 3). Por lo tanto es imposible realizar el paseo que Euler deseaba hacer en dichos puentes.

Fig. 11 Grafo que representa los puentes de Königsberg

Comentarios
Publicar un comentario